data("chickwts")
hist(chickwts$weight)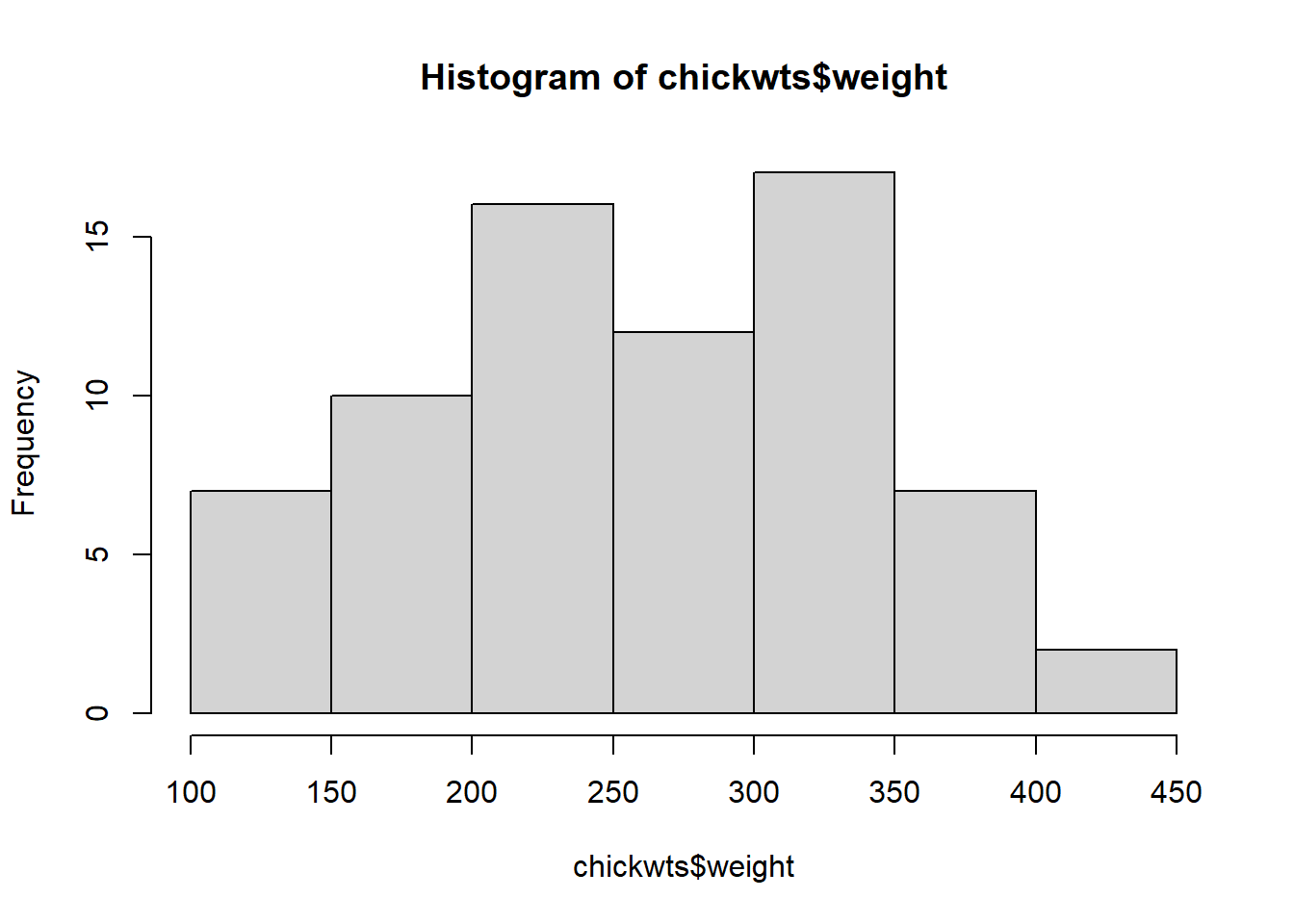
En esta clase, profundizarás en el concepto de distribución normal y en qué consisten las pruebas de hipótesis, como la conocida prueba T de Student.
Qu es la distribucion normal?
La distribución normal, también conocida como distribución gaussiana o campana de Gauss, es un modelo matemático que describe la distribución de datos en una población. Se caracteriza por ser simétrica alrededor de su media, con la mayor parte de los datos concentrados cerca de la media y una forma de campana.
Ejemplo: Nos interesa determinar si el peso de los pollos de crianza se distribuye de manera normal.
data("chickwts")
hist(chickwts$weight)
Basándonos en el gráfico anterior, ¿podemos concluir si existe una distribución normal? ¿Qué sucede si aplicamos otro método?
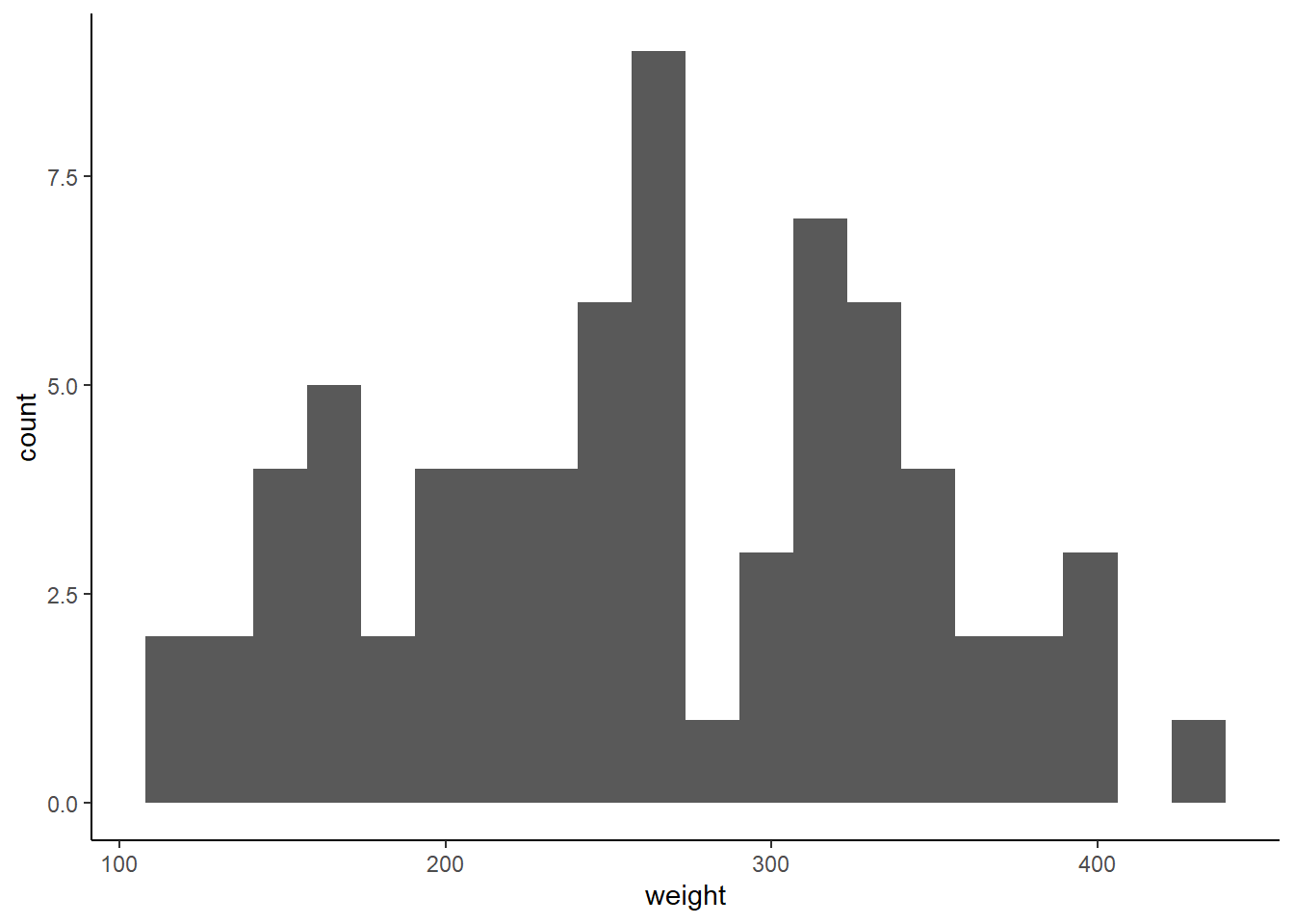
Y si mejor utilizamos una prueba estadistica?
Shapiro-Wilk normality test
data: chickwts$weight
W = 0.97674, p-value = 0.2101De acuerdo a la prueba de shapiro, el peso de los pollos de crianza presenta una distribucion normal. Pero, ¿Hemos aplicado correctamente la prueba de Shapiro para determinar si el peso de los pollos de crianza sigue una distribución normal?
En nuestro curso, aprenderás a aplicar e interpretar correctamente las pruebas de distribución normal, así como sus implicaciones.
Que es la prueba de hipothesis?
La prueba de hipótesis es un procedimiento estadístico utilizado para tomar decisiones sobre la validez de una afirmación o suposición acerca de una población. Se utiliza para determinar si existe suficiente evidencia en una muestra de datos para rechazar o no una afirmación sobre una característica de la población. En esencia, la prueba de hipótesis ayuda a los investigadores a tomar decisiones basadas en la evidencia recopilada en sus estudios, permitiendo inferir conclusiones sobre la población en general a partir de muestras específicas.
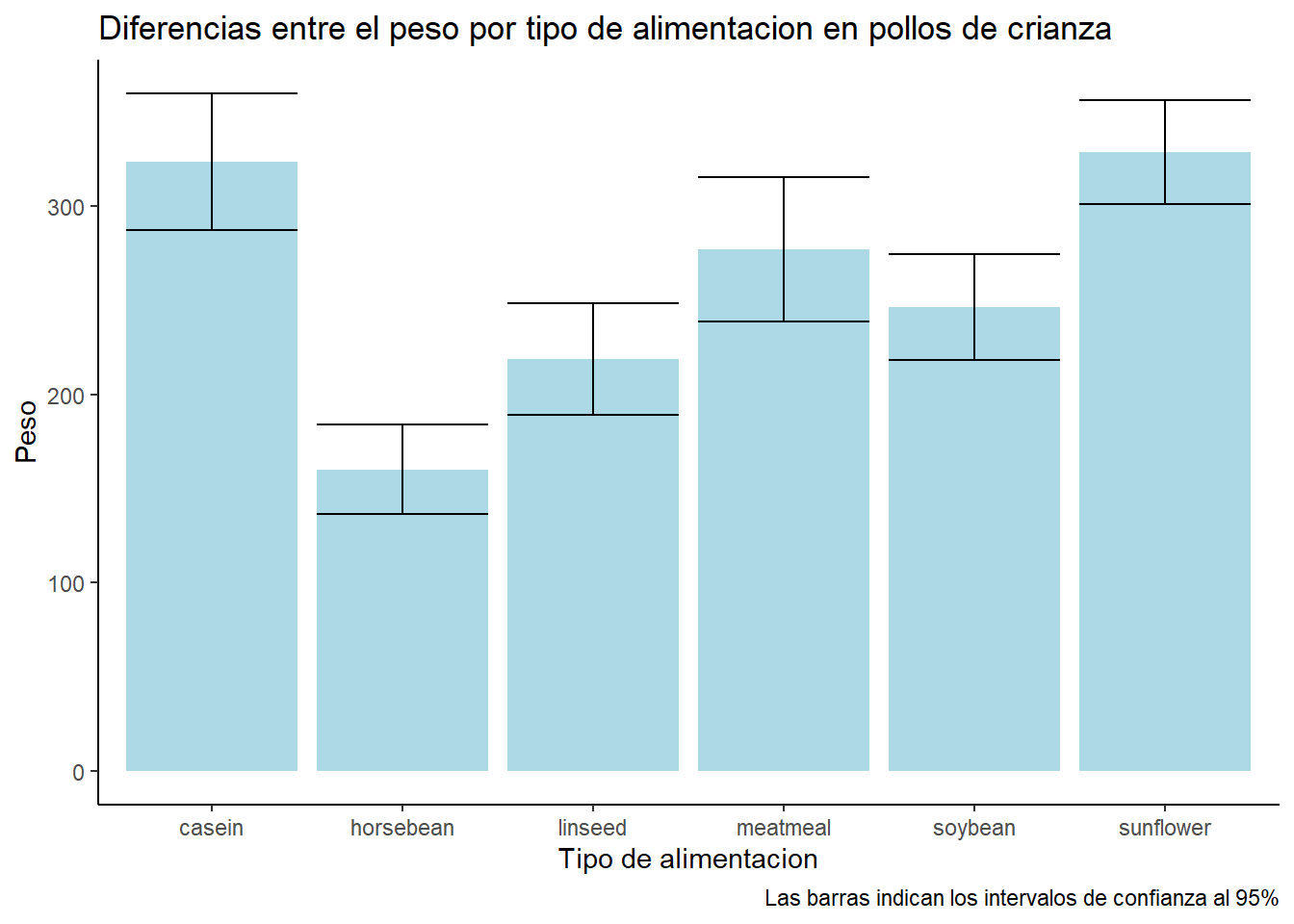
¿Qué sucede si aplicamos una prueba para determinar si el peso de los pollos de crianza difiere según el método de alimentación?
summary(aov(weight ~ feed, data= chickwts)) Df Sum Sq Mean Sq F value Pr(>F)
feed 5 231129 46226 15.37 5.94e-10 ***
Residuals 65 195556 3009
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1En este caso, los resultados proporcionan evidencia para afirmar que el peso de los pollos varía según el tipo de alimentación.
Sin embargo, ¿hemos aplicado correctamente la prueba de hipótesis? ¿Qué prueba hemos utilizado? ¿Cómo se interpretan los resultados? ¿Existen otras alternativas a considerar?
En nuestro curso, aprenderás todo lo necesario para abordar las incógnitas planteadas anteriormente.
Además, complementaremos los resultados con un gráfico apropiado.